Y = A
Y = /A
Y = A'
| IN | NOT |
| A | Y |
| F | T |
| T | F |
Binary Representations Home Page
(Last Mod: 11 January 2013 12:02:53 )
In the context of this discussion, words like "logic" and "logical" refer to a means of analyzing information based on the premise that each piece of information can only take on one of two values - True and False. Boolean Logic - also referred to as Boolean Arithmetic - is just a means of combining expressions involving variables that are restricted to these values.
The field of Boolean Arithmetic goes far beyond what will be covered here - this is merely a brief introduction to the basics.
We use Boolean Logic in everyday life all the time. For instance, we might have a personal policy about when to fill the gas tank in our car that says that we will fill it whenever we are below one-quarter of a tank but that we will also fill it if the price of gas is not higher than a certain amount provided we are also below three-quarters of a tank. If we were to express this more formally we would need three bits of information to make our decision plus an additional bit to represent the result of that decision. For instance, we might name our bits as follows:
Our logical expression is then:
(FillUp) = (LessThan1/4) OR ( (LessThan3/4) AND (NOT(HigherThanPrice)) )
The above expression uses what are considered the three primitive operators of Boolean Logic - NOT, AND, and OR. Each of these operators takes on the properties that we normally expect it to based on everyday usage. To formalize these, we explicitly state all of the possible combinations of input values and what the resulting output value would be for each combination. This is referred to as a "Truth Table".
Boolean logic can be expressed a number of different ways, the Truth Table being one of them. In addition, they can be expressed using Boolean Algebra in a manner similar to normal algebra, though with slightly different rules and conventions. Finally, Boolean operations can be shown graphically using "logic gates" and schematic diagrams showing the connections between them.
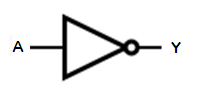
This operator has a single input, A. Its output, Y, has the opposite state as the input. This is frequently referred to as a logical inversion and the NOT gate is commonly called an "inverter".
In a Boolean expression, there are three common ways to indicate inversion, an overbar over the inverted quantity, a slash (both forward slash and backslash are used) before it, or an apostrophe after it. The overbar is generally preferred, but is not supported in most type fonts.
Like a minus sign in normal algebra, the NOT in Boolean algebra is the functional operator with the highest precedence, although parentheses and other grouping operators are higher yet, as in normal algebra.

| IN | NOT |
| A | Y |
| F | T |
| T | F |
This operator has two inputs, A and B. Its output, Y, is TRUE only if both of its inputs are TRUE.
It can be generalized to any number of inputs by following the rule that the output is TRUE only if ALL of the inputs are TRUE.
In a Boolean expression, the AND operation is represented similarly to multiplication, either by putting the two variables together or by using a "dot" between them. The "x" symbol is seldom used.
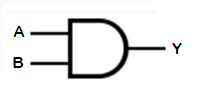
| IN | AND | |
| A | B | Y |
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
This operator has two inputs, A and B. Its output, Y, is TRUE if either of its inputs are TRUE.
It can be generalized to any number of inputs by following the rule that the output is TRUE if ANY of the inputs are TRUE.
In a Boolean expression, the OR operation is represented similarly to addition.
The choice of the multiplication symbol for AND and the addition symbol for OR is not coincidental. As in normal algebra where multiplication has higher precedence than addition, the AND has a higher precedence than the OR.
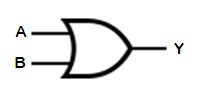
| IN | OR | |
| A | B | Y |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
It turns out that, in everyday usage, we actually use two meanings for the word "or" and usually rely on context to determine which is meant. For instance, a parent might tell a child that they will get grounded if they don't do their homework or if they stay out too late. In this case, it is understood that they will also get grounded if they don't do their homework and they stay out too late. In other words, they will get grounded if one or the other or both of the inputs are true. This is called an "inclusive-OR" because it includes as true the condition where both inputs are true. But that same child might get told at dinner that they can have ice cream or chocolate cake for dessert. In this case, we do not mean that they can have ice cream and chocolate cake. In other words, than can have one or the other but not both. This is called an "exclusive-OR" because it excludes from being true the condition where both inputs are true.
In formal logic, we can't allow the context of usage to determine which form is meant - we must be explicit. The two operators are called IOR and XOR for Inclusive-OR and Exclusive-OR respectively. In practice the term IOR is seldom used and it is assumed that OR is to be interpreted as IOR and that we will explicitly indicate when we mean XOR.
Although not as apparent as the AND and IOR operators, the XOR can also be generalized to any number of inputs by following the rule that the output is TRUE only if an odd number of inputs are TRUE.
In a Boolean expression, the XOR operation is generally expressed by an addition operator with a circle around it. While using the XOR operator in an expression can be useful and convenient in terms of conveying the logic embodied by the expression, the rules associated with manipulating an XOR are somewhat complicated and easy to perform incorrectly; this is largely a reflection of the fact that XOR is something of a "pseudooperator" that can be expressed in terms of the three fundamental operators of NOT, AND, and OR. Therefore, when manipulating Boolean expressions, it is common practice to expand the XOR operator into its more fundamental representation.
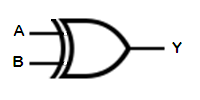
| IN | XOR | |
| A | B | Y |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | F |
Each of the two-input operators described above has a corresponding gate in which the only difference is that the output is inverted after performing the underlying operation.
This gate has two inputs, A and B. Its output, Y, is FALSE only if both of its inputs are TRUE.
It can be generalized to any number of inputs by following the rule that the output is FALSE only if ALL of the inputs are TRUE.
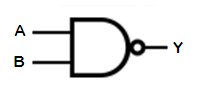
| IN | NAND | |
| A | B | Y |
| F | F | T |
| F | T | T |
| T | F | T |
| T | T | F |
This gate has two inputs, A and B. Its output, Y, is FALSE if either of its inputs are TRUE.
It can be generalized to any number of inputs by following the rule that the output is FALSE if ANY of the inputs are TRUE.
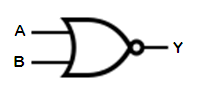
| IN | NOR | |
| A | B | Y |
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | F |
The XNOR gate is an inverted-output XOR gate. It's output is TRUE if both of its inputs are the same. Thus, it is frequently referred to as an EQUIVALENCE gate, or EQU gate. Like the XOR, it can be generalized to any number of inputs by following the rule that the output is TRUE only if an even number of inputs are TRUE.
In a Boolean expression, the XNOR operation is sometimes indicated by a dot with a circle around it, though this is not particularly common. Like the XOR, this is something of a "pseudooperator" that can be expressed in terms of the three fundamental operators of NOT, AND, and OR. Therefore, when manipulating Boolean expressions, it is common practice to expand the XNOR operator into its more fundamental representation.
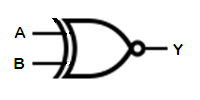
| IN | XNOR | |
| A | B | Y |
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
Like normal algebra, Boolean algebra is based on a number of properties that govern what manipulations can and can't be performed. These basic properties are shown below and, for the most part, are very similar to corresponding properties from normal algebra.
Remember that Boolean variables can only take on one of two values, namely True and False. The values are called by different names. The most common pairs of names for True are {True, T, High, HI, H, 1} and the most common names for False are (False, F, Low, LO, L, 0}. When working with Boolean algebra, the names {1,0} are particularly handy.
| PROPERTY | EXPRESSION | |
| Logical Inverse | 0 = 1; 1 = 0 | |
| Involution | (A')' = A | |
| OR | AND | |
| Indempotence | A + A = A | A ∙ A = A |
| Identity | 0 + A = A | 1 ∙ A = A |
| Complementarity | A + A = 1 | A ∙ A = 0 |
| Masking | 1 + A = 1 | 0 ∙ A = 0 |
| Commutivity | A + B = B + A | AB = BA |
| Associativity | (A+B) + C = A+(B+C) | (AB)C = A(BC) |
| Distributivity | A + BC = (A+B)(A+C) | A(B+C) = AB + AC |
The fact that OR distributes over AND, in addition to AND distributing over OR, seems unusual because we are accustomed to multiplication distributing over addition but not addition distributing over addition. It's important to keep in mind that we are not talking about addition and multiplication, we are talking about two very different operations, namely OR and AND. While it is useful that many of the properties carry over from normal arithmetic, which makes it very handy to reuse the same symbols for operators, it should also not be surprising that there are a few differences, as well. The distributivity of OR over AND is a consequence of the Indempotence and Masking properties, as shown below.
| A + BC | = 1∙A + BC | Identity of AND |
| = (1 + B + C)A + BC | Masking of OR | |
| = (A + BA + CA) + BC | Distributivity of AND | |
| = (AA + BA + CA) + BC | Indempotence of AND | |
| = (AA + CA + BA) + BC) | Commutivity of OR | |
| = (AA + CA) + (BA + BC) | Associativity of OR | |
| = (A+C)A + B(A+C) | Distributivity of AND | |
| = (A+C)A + (A+C)B | Commutivity of AND | |
| = (A+C)(A+B) | Distributivity of AND | |
| \ A + BC | = (A+B)(A+C) | Commutivity of AND |
The Indempotence and Masking properties also make some very useful, though non-intuitive, simplifications possible. Such as
AB + AB = A(B + B) = A
AB + B = AB + (A+1)B = A(B + B) + B = A + B
A + AB = A(1 + B) = A
Thus far we have been working only with logic values as abstract notions of "True" and "False". But a logic gate has to work with a physical representation of this notion and, when all is said and done, all it "knows" is the representation and it has no awareness of the abstract notion being represent. For example, most physical logic gates are designed under the assumption, known as "positive logic", that a low voltage will be interpreted as a "False" and a high voltage will be interpreted as a "True"; hence we design an OR gate so that it's output is at a high voltage if the voltage at either input is at a high voltage. Similarly, a positive logic AND gate is designed so that it outputs a high voltage if (and only if) the voltages at both of its inputs are high.
But there is nothing that mandates that we interpret a high voltage as a True; we could instead use "negative logic" in which a low voltage is interpreted as a True and a high voltage as a False. But making this choice does not change the physical behavior of the gates we have already designed -- our OR gate will still produce a high voltage if either of the input voltages are high and a low voltage only if both input voltages are low while our AND gate will still produce a high voltage if and only if both inputs are high. The only thing that has changed is the abstract logical notion that we associate with these levels. So let's look at those a bit closer.
| +OR Gate | Pos Logic | Neg Logic | ||||||
| A | B | Y | A | B | Y | A | B | Y |
| L | L | L | F | F | F | T | T | T |
| L | H | H | F | T | T | T | F | F |
| H | L | H | T | F | T | F | T | F |
| H | H | H | T | T | T | F | F | F |
| +AND Gate | Pos Logic | Neg Logic | ||||||
| A | B | Y | A | B | Y | A | B | Y |
| L | L | L | F | F | F | T | T | T |
| L | H | L | F | T | F | T | F | T |
| H | L | L | T | F | F | F | T | T |
| H | H | H | T | T | T | F | F | F |
This demonstrates that a positive-logic OR gate is identical to a negative-logic AND gate and vice-versa, namely a positive-logic AND gate is also a negative-logic OR gate.
Assuming all we have are positive-logic AND and OR gates (in addition to NOT gates, which are the same regardless of the type of logic and hence are their own dual), if we have a system that is using one type of logic (let's say positive logic), then we can easily convert that to the other brand of logic by inverting every signal and swapping all of the AND gates for OR gates and all of the OR gates for AND gates. A direct consequence of this is De Morgan's Theorems.
Among the most powerful and useful theorems of Boolean Algebra are De Morgan's Theorems. These theorems stem directly from the duality of Boolean logic and can be expressed as follows.
 |
↔ |
|
|
A+B = A∙B |
 |
↔ |
|
|
A∙B = A+B |
Simply put, these theorems state that you can swap an OR for an AND (or the other way around) as long as you invert all of the inputs and all of the outputs.
De Morgan's Theorms can be proven by direct enumeration of the truth tables involved. A proof using strictly Boolean algebra is straight forward, but relies on a subtle property. Namely consider that we have two Boolean functions X and Y. These are equal if and only if both of the following statements are true: Y is True under all conditions for which X is true, and Y is False under all conditions for which X is False. Now, consider the implication of showing that X+Y = True; this means that any time X is True, then X will be False, requiring that Y be True. Thus we have proven that Y is True under all conditions for which X is True. Similarly, consider the implication of showing that XY = False; this means that any time X is False, then X will be True, requiring that Y be False. Thus we have proven that Y is False under all conditions for which X is False.
Thus
X = Y IFF XY = F and (X+Y)=T
With this in mind, we want to show that
(AB) = (A+B)
We will set
X = (AB) and Y (A+B)
We then first examine
XY = (AB)(A+B)
XY = ABA+ABB
XY = (AA)B+A(BB)
XY = 0
We then examine
X+Y = (AB) + (A+B)
X+Y = [A+(A+B)][B+(A+B)]
X+Y = [(A+A)+B][(B+B)+A]
XY = 1
The second line of the last proof is the result of applying the distributive property of OR over AND, which is a property that is not consistent with our normal algebraic properties (since addition is not distributive over muiltiplication) and so this step looks awkward for most people.
De Morgan's theorems say nothing about how XOR behaves under duality, but it is easy enough to determine from first principles. A slightly modified rule results, namely that you can invert any subset of an even number of inputs and outputs without changing the logic. A special case of this is moving a bubble from one pin (either input or output) to another, since this is inverting two pins. Thus, you can rearrange the bubbles on an XOR (or XNOR) gate without changing the logic.
 |
↔ |
|
|
A Å B = A Å B |
In terms of logic duality, an even-input XOR is the dual of an XNOR while an off-input XNOR is its own dual. As mentioned previously, the behavior of XOR in Boolean algebra is sufficiently subtle and complex that it is generally best to replace it with its fundamental equivalent AND-OR equation/circuit and work with those, instead.
There are a couple of common mistakes that people make when working with Boolean Algebra. Perhaps the most common two are failing to recognize the following.
A B ≠ AB (i.e., (A')(B') is not the same as (AB)'
Similarly,
A+B ≠ A+B (i.e., (A')+(B') is not the same as (A+B)'
The first of these is particularly easy to make because it is easy to fail to recognize that the overbar is being applied individually to adjacent variables and not collectively to both. It is therefore critical that expressions using the overbar notation be clearly written. To aid in avoiding confusion, the judicious use of parentheses, even where not strictly needed, can greatly reduce the likelihood of making such mistakes. Thus the first of these could be written
(A)(B) ≠ (AB)
It is unlikely that the first would be mistaken for the second, especially if the parentheses extend vertically between overbars that apply to terms individually (which the fonts used above don't permit) and extend over the parenthesis surrounding expressions to which they do apply collectively.
The basic operators have some useful properties that can be exploited when developing logical systems - whether hardware or software based. Perhaps the three most fundamental of these properties is the ability to set, clear, and toggle a logical value using a "mask".
It is commonly the case that we have many bits that we can store logical values in but, because of the way our system is constructed, we can't read and write those bits individually. Instead, we have to read and write to a larger collection of bits, such as a byte or an even larger multi-byte value, simultaneously and as a whole. If we are going to work with individual bits under these conditions, then we must exploit the properties of the logical operators in such a way as to allow us to determine and/or change the state of one bit within a larger collection of bits without being affected by the state of any of the other bits and, just as importantly, without affecting the state of those other bits in the process. This is called "bit banging" and the material here provides the necessary understanding of the properties that need to be exploited in order to carry out useful bitwise operations.
In all of the discussions that follow, we will assume that we have a data bit, A, that we want to work with and a control bit, MASK, available to us. Let's look at the practical meaning of the basic logic operations in this context.
A = (A) AND (NOT (MASK))
- If the MASK bit is FALSE, then the value written to A is the same as what was already there.
- If the MASK bit is TRUE, then the value of A is cleared (forced to be FALSE)
A = (A) OR (MASK)
- If the MASK bit is FALSE, then the value written to A is the same as what was already there.
- If the MASK bit is TRUE, then the value of A is set (forced to be TRUE)
A = (A) XOR (MASK)
- If the MASK bit is FALSE, then the value written to A is the same as what was already there.
- If the MASK bit is TRUE, then the value written to A is the opposite of what was already there.
The important properties in each case is that (a) when the control bit is FALSE, the value in the data bit is left effectively unaltered regardless of what was originally stored there, and (b), when the control bit is TRUE the value written to the data bit accomplished some specific desired result regardless of the value originally stored.